Although the systems approach has become firmly entrenched in our current way of thinking, it can hardly be denied that we are a long way from having a truly general theory of spatial systems at our command. Not only do we have no comprehensive model or set of models that can be used to interpret spatial order, but also lacking is a general philosophical position within which practical investigations might be related to their more universal context. The works that follow address these issues at a very fundamental level. In them is outlined a philosophical approach to complex systems organization which, when extended to the level of operational modelling, provides both descriptive power and conceptual flexibility. The discussion begins here with an extension of some Rationalist philosophy concepts intended to provide a more useful basis for the study of complex systems. Following this is the presentation of a model of internal relations consistent with a "most-probable state" kind of logic and earlier-stated goals.

SOME ASPECTS OF THE PHILOSOPHY OF SPINOZA AND LEIBNIZ

    While Hegel (1770-1831) is often credited with laying the philosophical cornerstone for modern systems thinking with his doctrine of internal relations, I believe it is more productive to first turn one's attention to the seventeenth century philosopher Benedict de Spinoza (1632-1677) for the most profound treatment of nature as a general system. This is rarely done now, though Spinoza's ideas have historically had considerable influence on a number of notable thinkers (for example, Leibniz, Bergson, and Teilhard de Chardin). I shall not take the time here to attempt a defense of Spinoza's ideas as regards those of other philosophers but instead will plunge directly into a brief synopsis of concepts relevant to the present discussion.

    Spinoza is often considered quite modern in his views; in theory, at least, his method of inquiry reduces to a dialog between investigator and nature that is virtually devoid of metaphysics. Nonetheless, he was a firm believer in the existence of God. Spinoza's God, however, was inseparable from existence itself. This then-heretical pantheism was consistent with his view that nature as a whole constituted a kind of all-encompassing continuum he referred to as "substance." It was impossible for man to obtain any direct knowledge of substance, which existed under some number of "attributes" through which, one might say, its intrinsic order was expressed "in a complete and unbiassed form." Importantly, man has no direct sensible knowledge of these attributes either; instead, each is implicit in innumerable "modifications" which we can directly perceive and to which we attach various kinds of meaning. This point must not be confused: while it is our habit to think of the things that "fill space" as having properties such as color and weight that directly characterize their natural essence, Spinoza did not see things in quite this fashion. According to his way of thinking, a red rose is not an object with the attribute of redness; rather, it constitutes a finite element extending "redly" under the attributes thought and spatial extension. Note that measures describing the "spatial distribution" of roses do not necessarily give us more information about the attributes thought and spatial extension than do, say, measurements taken on their anatomical structures. On first contact this curious turn of affairs seems rather unhelpful in clarifying the meanings of "thought" and "spatial extension." It is not, however, because it focuses our attention in new and useful directions. Most importantly, it forces a critical re-evaluation of the tacit assumption that things "fill space." The Spinozian understanding of nature is instead one in which all directly manifest properties represent patterns of interaction underlain by common rules of organization referable to a more fundamental ordering process.

    Spinoza's model of natural order can be schematically diagrammed as follows:

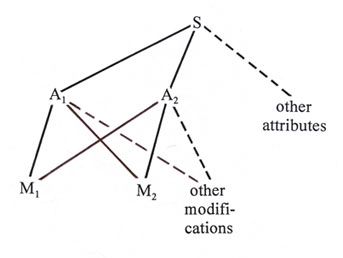
Figure 1

where S represents substance, A_i represents attributes, and M_i represent modifications. Note the branching structure involved: substance is both unique and all-inclusive and subsumes all attributes, to which in turn are referred an assemblage of virtually infinite numbers of modifications.

    Though extremely brief, the preceding description of Spinozian ideals forms an adequate base for what follows, which is not intended as an analysis of that philosopher's work.¹ Spinoza's ideas do, however, provide a useful point of departure for the discussion. Though appealing as a philosophical structure, the Spinozian view of nature contains a fundamental weakness that renders it difficult to apply to the study of real world situations. Spinoza apparently believed that it is impossible to isolate specifics from the continuum of reality; that is, each modification of an attribute is in some sense both unbounded and unrelatable to other modifications (perhaps because each is literally unique?). This interpretation of nature seemingly casts it as having order but no parts, or at the least no independently meaningful parts. This emphasis on "vertical" organizational principles makes it difficult to order our impressions of the "horizontal" links that form the major part of our day-to-day existence. The characteristics of interaction of finite entities such as human beings thus remain obscure in Spinoza's writings, or at best are disposed of in a manner not lending itself to practical analysis.

    In criticizing Spinoza's beliefs, the German philosopher/mathematician Leibniz (1646-1716) dwelled on the issue of the supposed indivisibility of nature.² Leibniz felt that not only was the whole of reality manifest in any given portion of it (as Spinoza also believed), but that these portions should be conceived as individual entities in their own right. This became the foundation for the "monad" concept, which provided for a kind of elementary particle in each of which was reflected the characteristics of all other such particles. In this view was the flexibility necessary for an interpretation of horizontal relationships in nature. It also permitted--as did Spinoza's ideas--hierarchical representation of nature. Nonetheless, Leibniz was unable to develop from this base a satisfactory model of how it was that any given monad actually contributed to a group structure that could mediate such universal symmetry. It is to a consideration of this matter that we first turn in the present study.

AN EXTENSION OF THE RATIONALIST APPROACH

    There seems little value in attempting to argue that the basic position of either philosopher is inherently more right or wrong than the other's. Rather, in what follows I have attempted to combine what I see as being critical positive elements of each position in such a fashion as to make possible new directions of study. This has necessitated some invention of new concepts; hopefully, the ends will be viewed to justify the means.

    Let us therefore begin with a few definitions (these will be retained from here on; more colloquial applications of the same terms will be especially noted). For present purposes, an "attribute" will be considered as that in virtue of which substance may be understood. This is in close accordance with Spinoza's definition of the term. Following Spinoza's views on the matter, I accept that while in theory any number of attributes might exist, human powers are limited to the recognition of but two: spatial extension and thought. Here, attention is focused on the development of ideas relevant to consideration of the second.

    A "modification" will be defined as a (the) sensible, or discrete, aspect of an attribute. This is also a very Spinozian manner of understanding, but contains beyond his view some implicit associations that will only become apparent after the remaining definitions are presented. At any rate, modifications are regarded here as entities occupying complete and delimitable domains. Probable examples of the myriad of modifications referable to spatial domains include: the distribution of organisms, cities, continental crust (sial), etc.; cells; and organisms.

    We next turn to "modes." These are to be understood as quasi-finite subunits or classes of subunits resulting from the internal differentiation of a given modification (i.e., its natural subsystemization). The implications of this definition are considerable here, because I will suggest shortly that modifications differentiate internally in a manner having regular properties. Probable examples of sets of modes would include faunal and floral regions, the individual continental masses, and the organelles and organal systems making up individual cells and organisms, respectively.

    The last term introduced at this point is "representation." This is to name those characteristics of the internal relational order of attributes that are expressed in the organization of modes; that is, that prescribe the way modifications internally differentiate as modes. We may thereby speak of the "representation" of an attribute in its various modifications. Following Spinoza, I accept that all modifications referable to the two main attributes in some fashion reflect the basic nature of those attributes. From that starting point, it is natural to consider what the relation between attributes and modifications may be that allows this to be so. In accepting the Leibnizian position that any given modification of an attribute is somehow reflected in any other given modification, we are likewise led to question what it might be that all modifications have in common that could make this possible. In the system presented here, the holistic and "monadic" positions of Spinoza and Leibniz, respectively, are integrated through the use of the notion of representation. Simply, "attribute" is the name given to rules of representation that actualize the infrastructure of modifications. These rules are therefore viewed as being implicit in any modification. This solution is consistent with Spinozian reasoning, which leads to the conclusion that there exists but one set of rules referable to each attribute through which modifications may be characterized. It also yields the idea that in each modification is reflected the fundamental nature of all other modifications: things cannot be otherwise if, as we assume here, all modifications differentiate into their characteristic observed forms on the basis of the same relational structure. We are thereby provided with a tangible link to Leibniz's "monads."

    This way of viewing the organization of the natural world has profound implications for the way problems of spatial distribution and diversification must be treated. Space itself is no longer viewed as having directly evident (or perhaps better put, "naïvely evident") qualities; rather, it becomes in effect a system of relations of which there can probably be no single absolute rendering. To avoid confusion, it is necessary to recognize two kinds of "space", varieties which may be termed "relational" and "sensible". The former refers specifically to the attributes spatial extension and thought and to their conditions of internal relational order. The latter may be taken as the sum of sensible spatial domains occupied by modifications of the attribute spatial extension. Through this separation of terms, the general and observable "facts" of distribution of things--including the notion of "spatial pattern" itself--are referable only to sensible space; the fundamentals of their organization into spatial systems, however, must be interpreted as a function of the characteristics of relational space.

   This conceptual separation of space into sensible and relational components will inevitably lead to some initial confusion that must be overcome before these "Neo-Rationalist" concepts can be successfully applied to considerations of real world conditions. Especially troublesome may be the fact that it is possible for two modifications to exhibit the same sensible properties of extension (i.e., have the same spatial domain) but be comprised of modal systems of entirely different areal differentiation. An example related to some of my own work on zoogeographic regions may aid in appreciating this point.³ Suppose we are considering the two modifications "terrestrial mammal distribution" and "terrestrial animal distribution." The spatial domains of these two modifications are essentially identical for the reason that virtually all exploitable terrestrial habitats that exist are inhabited by both mammals and animals in general. We must not jump to the conclusion, however, that the system of modes (regions) into which each has differentiated to maintain an internal relational structure consistent with that of the underlying attribute need be areally identical. The biogeographic histories of the two groups are not identical (mammals, of course, having evolved much later than animals taken as a whole), and must be viewed as responses to generally different sets of proximate causal influences when viewed within their sensible space context. Nonetheless, according to the understanding being developed here we can still believe that these two histories have devolved from a single relational ordering process implicit in the attribute. In so doing, we attribute to nature the capability of producing structures that are unique with respect to their characteristics of occupation of sensible space, but isomorphic with respect to their fundamental organizational properties.

    A related candidate for confusion is the difficulty that it seems particular modes might be associated with more than one modification. For example, though we might determine "Australia" to be a region (mode) within a faunal regions system depicting mammalian distribution (a modification), one might argue that this areal unit also hosts non-mammalian faunal elements and thus should be considered to contribute, ipso facto, to understandings of the organization of other world faunal distribution patterns. Recall, however, that the function of a modification and its modes can be described in no other way than through the structure of relational space, not sensible space. It is therefore immaterial that Australia may be "in the same physical place" with respect to two modifications; what is significant is whether it is expressive, as a sensible natural unit, of the relational structure of each (of course, a given sensible space unit such as Australia could qualify as a mode in more than one modification; the point, however, is that it does not have to).

    Neither can we view modifications of small spatial domain as in some fashion being "enclosed by," or existing as a subset of, modifications of larger spatial domain. The spatial domain of the distribution of the class Mammalia, for example, is much larger than is the spatial domain of the distribution of any given mammal species, but we are obliged to recognize in each a modification of equal and independent status. There are no systematic affinities among modifications (nor between the modes of different modifications), except possibly in the sense of their historical order of derivation.

    Lastly, each modification is relatable to both primary (at the least) attributes, as otherwise it appears we will be guilty of violating the notion that each attribute provides "complete and unbiassed" representation of sensible structure.

    Perhaps the most straightforward question that might be raised regarding these new ideas is why, given that it is posed a single organizational basis underlies all modifications, there should be so much observable variety in our surroundings. This question is best answered by reading the rest of these two works; for the present, it can simply be noted that we have no reason to expect that the rules of representation underlying the attribute spatial extension should be directly expressed in the sensible characteristics of the spatial domain. (Consider the analogous idea that while a particular integer has no direct expression in sensible space, it can still be used as a logically consistent means of labelling a certain quantity of entirely different objects.)

    To recap our conceptual revision of the basic Spinozian model, the above comments have been diagrammatically represented in Figures 2 and 3. In both figures, attributes are assumed to bear the same general relation to substance described through Figure 1. Specifying (that is, both describing and exhausting its domain) M₁ in Figure 2 is the "hierarchical class" H₁ of finite modes m_i. Lines interconnecting modes 1 through 3 symbolize the relational system uniting them into H₁ with respect to A. The boundary of M₁ is dotted where it is not a part of a finite mode within H₁ because M₁ does not exist as sensible space where it is not expressed through H₁ (actually, H_i in general). Again, this extension of the Rationalist view seems to do no great violence to Spinoza's original way of casting things, but at the same time responds to the criticisms of his system made by Leibniz. An advantage of this conceptualization, moreover, is that it is particularly conducive to canonical hierarchical representation; i.e., a particular hierarchical class structure can be collapsed into a hierarchical class specified by a more inclusive set of internal relations. As indicated in Figure 3, the system of primary modes of Figure 2 might be combined in a fashion yielding a system of "second order" modes, a construction subject to the condition that the newly devised level of order be self-specifying at both its own level and the original one. This calls for a strategy of modal grouping that retains such relationships, a subject taken up shortly.

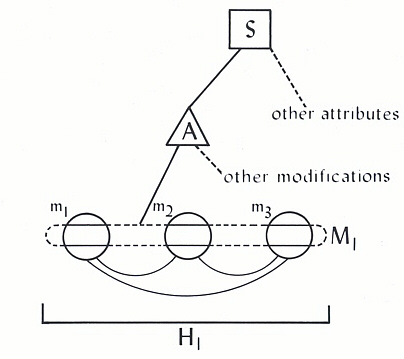
Figure 2

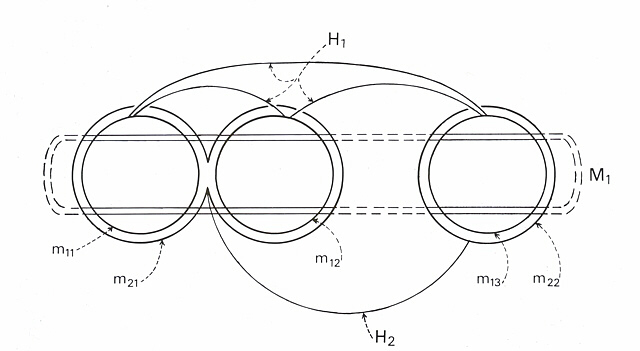
Figure 3

THE EMPIRICIST TRADITION VERSUS RELATIONAL ANALYSIS

    It seems advisable to stand back for a moment to reflect on where we have been thus far and where we are going next. Faithful to the Empiricist tradition, it has become the norm to believe that the objects we choose to study exhibit attributes (in the more common sense of the word) that can be measured and reflected upon to give us direct knowledge of "underlying" reality. Thus, we now tend to believe it meaningful to consider "occupying space" and exhibiting measurable qualities to define space directly on the basis of those qualities. Following Spinoza, I do not believe this approach can produce an efficient representation of worldly structure and process. Order, I suggest, is not most fundamentally manifest at the sensible level as a geometry involving objects; rather, it is a characteristic of the internal organization of the unobservable (namely, attributes--and note that I do not disallow the possibility of using geometry as an aid in understanding these). An attribute may be thought of as a particular kind of relational structure whose reflection in observable natural form is best represented by the notion of the modification. Should we wish to apply a theoretical understanding of the rules of representation within attributes to the sphere of the practical, therefore, we must first determine in what manner modifications internally differentiate into systems of functionally interdependent modes.

    A few examples of the general kind of thinking I am suggesting might be beneficial here. We can first return to zoogeographic stuedies. Regional faunas develop as complex interplays between regimes of isolation (during which unique evolutionary lines develop) and regimes of physical connectedness (during which interchange of populations takes place). At any given time, the cumulative results of such processes are manifest in sensible space as an overlapping array of distributional ranges of populations. Individual populations within this array may be restricted to a particular region or found in several. On the basis of the distribution of such commonalities (which may be represented in matrix form as an array of similarities coefficients), the characteristics of each region can be stated in a way that in effect specifies a set of relations. Similarly, the development of an "organism" is predicated on, literally, organization: the manner in which organal systems develop in a functionally interrelated way. In so doing, they constitute an internal ordering of relations that operates as a three-dimensional entity--a body--under one of the fundamental attributes. [I originally assumed this to be the attribute "spatial extension," but subsequently came to recognize it as "thought": a nonintuitive correction, but one which will be explained later.]

    If we wish to do more with this basic scheme of natural order, our attention must therefore be drawn to: (1) identifying the rules that order modifications internally in such a fashion as to constitute hierarchical classes; and (2) showing how the fact of such ordering can be interpreted within the real world of measurable qualities. Meeting these goals involves setting out logical criteria for the ordering of subclasses, and then translating this understanding into a framework within which metric (sensible space) interpretations are possible. I have not yet addressed the matter of the actual nature of modal differentiation; i.e., what specifically are the relational rules under which a modification organizes? Before we can attend to real world problems, it is necessary to start with an idea of what we believe should be the characteristics of relational space. The study of mammalian regionalization patterns, for example, therefore begins with a concern about the meaning of "varies over space" rather than any characteristics of the specific groups that are varying, including their distribution in sensible space. Ultimately, this concern should lead us to a particular delineation of structure upon which to base applied understandings of the modification "mammalian distribution." In related applications of such a system I would therefore be making use of an implicit relational structure to shed light on the manifest properties of the distribution of mammals, which is explicit within its spatial domain.

    We now turn to a consideration of the meaning of "appropriate" systems of representation; i.e., ones that might be argued to mirror the internal relational structure of the fundamental attributes.

A MODEL OF HIERARCHICAL INTERNAL RELATIONS

    The model of relational space about to be offered is predicated on Einstein's "lazy universe" principle: that universal change always follows the route of least resistance (thereby conserving energy). Thus, we might speak of the relational structure underlying thought as being one out of which "unlikely" states of matter are produced in the most likely way. This last concept is not by any means novel; for a discussion of the relevant physics, the reader is referred to the literature on irreversible thermodynamics.⁴

    I am thus taking as a starting point here the notion that organized structure in nature has fallen out in a manner referable to a most-probable-state kind of process. Our task therefore becomes to suggest a hierarchical structure of relations whose component sets of modes (hierarchical classes) describe such a state.

    We can begin our consideration of this kind of hierarchical ordering by asking the simple question "Given n objects about which we know nothing, what is the most likely number of classes into which these n objects can be grouped?" This elementary problem in combinatorial mathematics may be symbolized as max and is solved by finding the maximum value of S given by:

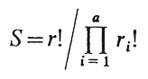
    We can enliven the discussion a bit by giving it a more relevant context. Given that n equals "number of subclasses" and r equals "number of classes into which n may be grouped", what values of n and r may be associated with one another such that these will yield maximum values of S for a given n? The most famous example of this type of problem is in statistical mechanics, where n is the total number of units of energy available to an isolated system and r, the number of elementary particles absorbing those units. It is assumed that these particles can attain various levels of excitation within the system; the total energy of the system is thus absorbed through certain numbers of particles attaining certain excitation levels. For any given combination of n and r, most-probable-state solutions for the number of particles falling into each excitation level can be worked out (this distribution is approximated by Boltzmann's Law). It is almost possible to translate this example directly into terms appropriate to the discussion here, as "number of units of energy available" becomes "number of subclasses", "number of elementary particles in the system" becomes "number of classes", and "excitation level" becomes "number of subclasses in a given class". One important difference between the two situations exists, however: our relational structure can include no analog to the "ground state" condition (excitation level zero) in statistical mechanics, as it is clearly illogical to permit a class containing zero subclasses to exist within an inclusive hierarchical structure. Thus, the distribution of classes that can be grouped from some initial number of subclasses is of truncated nature.

    A short example is perhaps useful. Under the conditions stated, it turns out that seven subclasses can be grouped into four classes in more ways (equals more probably) than seven subclasses can be grouped into any other number of classes. This is detailed as:

This configuration of one class with three subclasses, one class with two subclasses, and two classes with one subclass, may be arrived at in 4!/1!1!2!, or 12, ways. Recalling Figure 3, however, we need not stop at this first ordering of subclasses. Our four classes can be further grouped into some most probable number of still more inclusive classes. This turns out to be three, for which the details are:

    It is apparent that a ladder of subclass-class relationships may thus be generated in which any initial number of subclasses is canonically grouped through x steps to one all-inclusive class. Below are listed all the class inclusion series for initial values of one through ten meeting the maximum likelihood conditions just set out. Note that some outcomes are equiprobable, necessitating the expanded listing:

    None of this would be especially intriguing were it not for the fact that it is possible to isolate structural solutions for the above groupings that maintain most probable-state characteristics across all levels of the grouping structure. This can most easily be appreciated through the aid of dendrograms of the hierarchical relationships involved. A possible dendrogram representation of the seven subclass-four class configuration discussed above is:

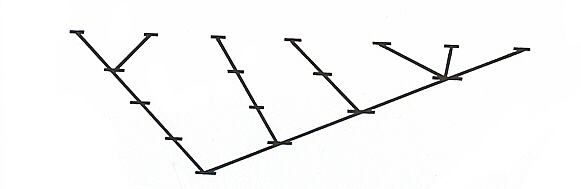
Figure 4

This shows how seven "first-order" (sub)classes group most probably into one second-order class containing three first-order (sub)classes, one containing two sub(classes), and two containing one (sub)class. But it also suggests that these seven first-order classes group into three third-order classes, two fourth-order classes, and one fifth-order class. Moreover, implicit in the diagram is the idea that the four second-order classes group into three third-order classes, two fourth-order classes, and one fifth-order class. Further, the three third-order classes group into two fourth-order classes and one fifth-order class and the two fourth-order classes group into one fifth-order class. Diagrammatically, the inclusion series may be represented on a "by-order" basis as:

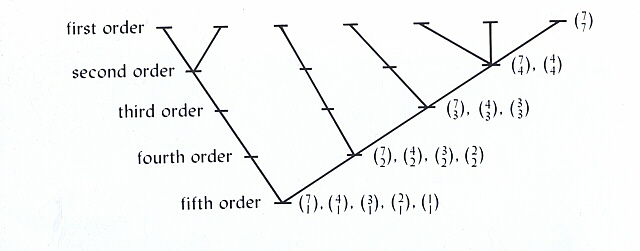
Figure 5

    Now it so turns out that each of the orderings represented in the particular "7-4-3-2-1" series depicted above is the most probable such ordering (for example, the ordering in the dendrogram above produces fourth-order classes containing three and one subclass, respectively, and this is what is required under maximum likelihood conditions). This is therefore what might be referred to as a "maximum likelihood tree". That such a relational structure exists is significant for our overall discussion, because: (1) it provides a reasonable interpretation of the system of canonical representation demanded by our earlier-developed concept of the hierarchical class, and (2) it satisfies our hope that a combined structure of horizontal and vertical relations can be stated in most-probable-state terms.

    There are a relatively small number of trees that satisfy this most-probable-state canonical hierarchic inclusion criterion. The solutions for initial (sub)class values of up through seven are given in Figure 6:

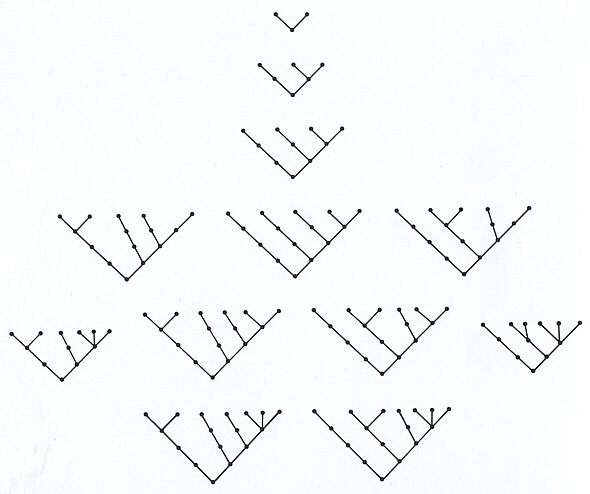
Figure 6

    A feature of this canonical inclusion series of considerable interest is the way that two initial subclasses (or a more extended series that has been collapsed to the stage of two subclasses) behave as collapsed a final time. It turns out that two such subclasses group equiprobably into one class of two subclasses or two classes of one subclass each. The tree structures involved, however, are of course identical. This is curious, because it seems to indicate that we must interpret what for all apparent purposes are identical structural outcomes as being logically different from one another. The solution to this dilemma seems to be to recognize in these alternative class structures another aspect of the hierarchical nature of unity itself. Given only two subclasses at the outset, there can be no way to compare one to anything else in a way which is different from an analogous comparison to the other.⁵ As a result, we are obliged to view a pair of subclasses as being both complementary images of one another and a single whole. Left and right, East and West, negative and positive electrical charges, the complementary helical strands of the DNA molecule, and male and female provide some real world examples of this condition. There are important philosophical ramifications of this interpretation. Since any initial number of subclasses can ultimately be hierarchically grouped to unity, this means that any degree of initial complexity of elements can be reduced to an interpretation based in structural isomorphisms. This will be true, moreover, wherever a bifurcation in the tree of structure exists-that is to say, everywhere (the apparent special case of "bushes" presents no problems for this interpretation; see below). Spinoza's and Leibniz's basic view of the unity of nature is thus supported in another way, because it can be seen that it is impossible in such a universe to have an entity that is other than a reflection of another such entity, in association with which it constitutes a logical whole.

    To this point, our dendrogram representations of most-probable-state hierarchical relations have been constrained in a way that is probably overly restrictive. For example, in Figure 5 it can be seen that all first-order subclasses that group together at the second-order level of integration do so at the same distance up the tree. On the basis of ideas set out so far, I see no reason why this additional requirement need be met in a maximum-likelihood tree. Bushes such as that evident in the first-order level of the tree in Figure 5 may thus contain latent structure within a given hierarchical level; to maintain the whole system of relations, however, it is necessary to ignore such latent structure and understand each subclass involved as being logically equivalent.

    With this refinement, we are in a position to identify the complete set of maximum-likelihood trees that exist. These are portrayed in Figure 7. Eleven appears to be the highest number of initial subclasses that can be integrated into a maximum-likelihood tree. Arrows within the diagram indicate the "lineage" of derivations associated with increasing complexity.

    Figure 7 shows that it is possible to construct a reasonably complex and internally-logical hierarchical system of class-subclass relations out of a bare minimum of initial constraints. Note, moreover, that even the limitation of eleven initial elements in the system is not much of a constraint, since any degree of further elaboration of structure within each initial subclass is non-contradicting as long as: (1) such elaboration is recognized as being irrelevant to the logical status of that subclass, and (2) it is understood that such elaboration can contribute to no further hierarchical ordering within the system.

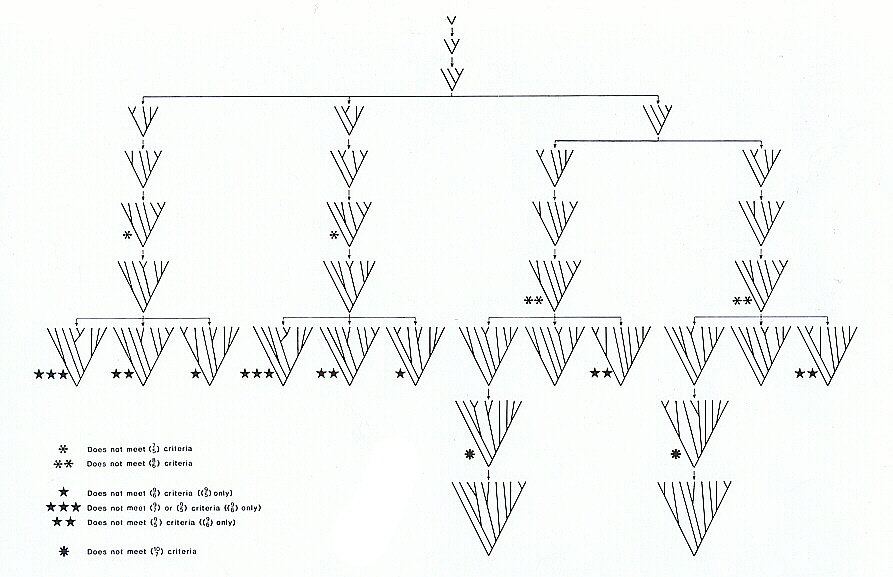
Figure 7. Dendrogram representations of all maximum-likelihood trees as defined in the text. Arrows indicate "lineages" of derivation. A number of the level nine trees do not produce maximum likelihood class structures for both max and max conditions: these are especially noted. In addition it is noted that several of the trees represented are unable to produce maximum likelihood class structures for certain other combinations, but as the latter do not directly contribute to the hierarchical inclusion series as here defined, the importance of this is debatable.

*                *                *

FINAL REMARKS (written October 2006)

    When I first deduced the preceding relational structure in the 1980s, I believed I was working out a representational system referable to the Spinozian attribute "spatial extension": simply, it seemed that all natural systems that "fill space" might present evidence of having differentiated out according to the "lazy universe" principle. Actually, however, such expressions of subsystemization, while apparent in many systems, seem to have more connection to the one-of-a-kind histories of differentiation of the subunits than they do to any underpinning principles of spatial extension per se. I have since concluded that this "lazy universe" kind of relational subsystemization is more likely to correspond to the Spinozian attribute "thought"--perhaps better thought of as "history"--than it is to "spatial extension."

    In the preceding writeup I have mentioned examples of modifications that seem to display the kind of dynamic subsystemization over time that such a relational structure would call for, including human bodies and faunal regions. To these might be added individual trees (especially, their branching patterns) and drainage basins (with their dendritic pattern of stream tributary development). But perhaps the best single example may come in the form of the several main tectonic plates that interact dynamically to comprise the geologic surface zone, the crust, of the earth. Now these are ostensibly in something approaching dynamic equilibrium (considering the time scale) with regard to their relative creations, expansions, and subductions, and it might be interesting for someone to take a look at the specific patterns of creation/evolution of these units--depending on how one counts, there are just seven main ones--relative to one another; i.e., do they fit the pattern of relations described in Figure 6 (or even Figure 7, if smaller pieces are also taken into account)?

     Not long after coming to these various conclusions as to how a "history" attribute might internally arrange itself, I started thinking more about the notion of spatial extension itself. Some conclusions on this matter are summarized in the next essay, originally written about ten years ago.

REFERENCES

1. For treatments of Spinoza's philosophy, see: J. D. Collins, Spinoza on Nature. Southern Illinois University Press, Carbondale, Illinois, 1984; G. W. Kashap (ed.) Studies in Spinoza. Univ. of California Press, Berkeley, etc., 1974; and P. Wienpahl, The Radical Spinoza. New York University Press, New York, 1979.

2. G. W. Leibniz, Discourse of Metaphysics/Correspondence with Arnauld/Monadology (translated by Dr George R. Montgomery). The Open Count Publishing Company, La Salle, Illinois, 1979.

3. C. H. Smith, "A system of world mammal faunal regions. l. Logical and statistical derivation of the regions". J. Biogeogr., 10, No. 5, 1983, pp. 455-466; C. H. Smith, "A system of world mammal faunal regions. II. The distance decay effect upon interregional affinities." J. Biogeogr., 10, No. 6, 1983, pp. 467-482; C. H. Smith, "Areographic representation of faunal characteristics through a 'second order' relational approach." Evol. Theory, 6, No. 5, 1983, pp. 225-232; and in preparation.

4. See, for example, L. von Bertalanffy, "The theory of open systems in physics and biology." In: Systems Thinking, edited by F. E. Emery, Richard Clay (The Chaucer Press) Ltd., Bungay, Suffolk, England, 1976, pp. 70-85; L. von Bertalanffy, General Systems Theory. George Braziller, Inc., New York, 1968; D. R. Brooks and E. O. Wiley, "Evolution as an entropic phenomenon." In: Evolutionary Theory: Paths to the Future, edited by J. W. Pollard, John Wiley and Sons, London, 1984, pp. 141-171; D. R. Brooks and E. O. Wiley, "Nonequilibrium thermodynamics and evolution: Responses to Bookstein and to Wicken." Syst. Zool., 34, No. 1, 1985, pp. 89-97; A. S. lberall, "On organization and the arrow of time." General Systems Yearbook, 21, 1976, pp. 141-144; E. Laszlo, "A general systems view of evolution and invariance" General Systems Yearbook, 19, 1974, pp. 3743; G. Nicolis and I. Prigogine, Self-Organization in Nonequilibrium Systems. John Wiley, New York, 1977; I. Prigogine, Introduction to the Thermodynamics of Irreversible Processes. Interscience Publishers, New York, 1961; W. Yourgrau, A. van der Merwe, and G. Raw, Treatise on Irreversible and Statistical Thermophysics. Macmillan, New York, 1966.

5. M. D. Mesarovic and D. Macko, "Foundations for a scientific theory of hierarchical systems." In: Hierarchical Structures, edited by L. Whyte, A. G. Wilson, and D. Wilson, American Elsevier, New York, 1969, pp. 29-50. Note that this implies bimodally-differentiated modifications also provide no basis for the representation of the attribute spatial extension.

_________________________

Continue to Next Essay
Return to Writings Menu
Return to Home

Copyright 2006 by Charles H. Smith. All rights reserved.
Materials from this site, whole or in part, may not be reposted or otherwise reproduced for publication without the written consent of Charles H. Smith.

Feedback: charles.smith@wku.edu
http://people.wku.edu/charles.smith/once/syst1.htm