The Once and Future Wallace
Discussion of the Spinozian Attribute "Spatial Extension"
INTRODUCTION
In papers published some years ago I introduced a model combining aspects of the philosophy of Benedict de Spinoza (1632-1677) with modern systems theory concepts [Smith 1986a, 1986b, 1987]. The 1986a paper has just been reproduced here in highly abbreviated/edited form: that is, both to express what I now feel to be its relevant aspects (to study of the Spinozian attribute "thought"), and to serve as a logical introduction to this discussion, which deals with the Spinozian attribute "spatial extension." The model leads to empirically examinable predictions, and following this writing we will take a look at a number of these.
Nothing more pervades everyday awareness than the notion that the three-dimensionality of the world we perceive is not distinct from the physically relative locations of the objects "contained within it." On first consideration this seems a safe assumption; on the other hand, it is by no means a trivial question as to how three-dimensionality per se arrives as an apparently primitive condition. In the present study extended space is interpreted as a derivative outcome: as the dynamic equilibrium resolution (and projection) of relationships within and among the individual subsystems which as a group comprise any delimitable system. The "relationships" here posed are of a type allowing for individual uniquenesses, yet reflecting a certain universal commonality--i.e., the properties involved are common to all such systems and project accordingly as a single, uniform result: three-dimensionality. Another way of stating the concept is to suggest that subsystemization itself represents both the cause and result of spatial extension, because there are rules underlying this sub-differentiation that are genetically synonymous with the fact of three-dimensional projection.
PHILOSOPHICAL FOUNDATIONS
Spinoza is not frequently consulted these days for advice on the nature of space; though philosophically elegant, his ideas on natural organization have steadfastedly resisted application within an applied, physical context. Moreover, and even more significantly, it was only shortly after his time that Locke and others provided such a context based on other presuppositions. Most efforts have gone into exploring the implications of the latter route--Empiricism--ever since.
Spinoza's concept of spatial extension in effect admits an additional structural level into the fundamental framework of natural organization. While we habitually view things that "fill space" as having properties such as color and weight that directly characterize their physical essence, Spinoza saw the situation rather differently. In his Ethics he set out an elaborate series of proofs beginning with the concept of a prior "essence of existence"--which he termed "substance"--the ultimate nature of which is implicitly beyond human powers of perception or appreciation. "Substance" thus has no accessible properties as such, and is perhaps best portrayed in pantheistic terms.
In Spinoza's system, substance is understood as "operationalized" (my term) through some number of "attributes" (his term) that constitute, as it were, governing rules of expression; i.e., it is these rules that actualize substance in a fashion creating a worldly milieu characterized, ultimately, by individual objects with directly tangible properties. Spinoza believed that there might be any number of such attributes operating, but that human powers are limited to the appreciation/recognition of but two: "thought" and "spatial extension." It must be emphasized that the two primary Spinozian attributes are not physical properties in the sense that "color" or "weight" are in the Empiricist tradition; instead they are better viewed as entirely cryptic organizing principles--thus the notion of the "rules of expression" mentioned above. Further, present-day thinkers are advised to allow the concepts "thought" and "spatial extension" as appropriated by Spinoza a good deal of room: clearly, his designation of these terms only very imperfectly hints at current usage, either in general, or in my writings here. Within Spinoza's natural system there is also terminology to describe the tangible reality to which we actually attach meaning (as constructed on the basis of the evidence of our senses): he referred to the elements of this as the "modes" and "modifications" of the particular attributes.
Spinoza's model of natural order can be diagrammed schematically as given in Figure 1, where S represents substance, Ai represents attributes, and Mij represents modifications. Note the branching structure involved: substance is both unique and all-inclusive and subsumes all attributes, to which in turn are referred an assemblage of infinite numbers of modifications.
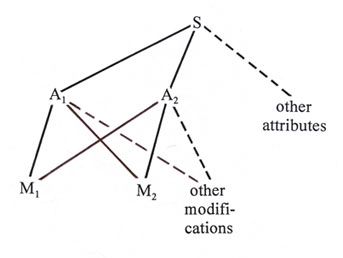
Figure 1.
No one has ever (to my knowledge) been able to suggest and empirically defend a working model of reality based on this conceptual structure. Complicating the picture is that Spinoza apparently argued that it is impossible to isolate specifics from the continuum of reality--that is, each modification of an attribute is in some sense both unbounded and unrelatable to other modifications. This interpretation of nature seemingly casts it as having order but no distinct parts, or at the very least parts that extend infinitely. Gottfried Wilhelm Leibniz (1646-1716) attempted to amend Spinoza's position with the "monad" concept, which provided for a kind of elementary particle in each of which was reflected the characteristics of all other such particles. Both men's positions support a hierarchical representation of nature and are to a considerable degree complementary--Leibniz's view does not contradict the idea of there being universal "rules of order," while Spinoza's tacitly accepts the possibility that one might yet be able to "see the whole of the universe in a flower."
Importantly, Spinoza argued that each attribute, independently, provides a "complete" (i.e., unbiassed and exhaustive) expression of the underlying essence, substance. If we are to follow Spinoza's lead, therefore, one of our first chores is to fathom how it might be that tangible reality can reflect the underlying essence in response to "rules of expression" of not only one, but both attributes (i.e., thought and spatial extension) simultaneously.
My extension of these ideas is actually rather straightforward. I have conceived each "modification" of a given attribute as reflecting an internal organization into subsystems according to a set plan. This "set plan"--not the overtly manifest properties of the individual system entities themselves--constitutes the underlying attribute. In this way the subsystemization of all extended space entities takes place as a condition/function of "rules of expression" that are common to all such subsystemizations. This commonality, I thus suggest, is the attribute itself, which thereby expresses itself, ipso facto, in all of its modifications. This solution, while still being remote from an immediate connection to physical existence, at least seems to answer to the main demands of Spinozian/Leibnizian doctrine.
Spinoza seemingly does not rule out the possibility that the two fundamental attributes are in some fashion relatable; he only insists that each be, as independently conceived, "complete" (exhaustive and unbiassed) with respect to its representation of substance. There are various ways of imagining how such a form of representation might operate, but a detailed treatment at this point would pull us too far off the present track. For the sake of example, however, one can note that: (1) a deterministic and matching kind of complementarity might so serve (as in, for example, the DNA molecule, in which from one-half of the double-helix structure one can determine the complete character of the other half), as could (2) conspatially alternate internal groupings of the same primary elements (as in the regional population system example set out below). I favor as more likely the second condition, and in the rest of the discussion a model based on one such understanding is entertained.
In the paper preceding this one my use of the term "natural system" was meant as a near synonym to Spinoza's "modification," and I used Spinoza's own term "mode" in parallel fashion as my name for the subsystems whose relations with one another sustain the encompassing system by observing the "rules of order" constituting the attribute. In that work I also explained a rationale for believing that such modes may be hierarchically organized. I then produced a most-probable-state (and set theory) based model for such an inclusion series, arguing that this represents a conservative starting point for trying to get at the nature of the hierarchical relations involved. Following all this out produces the inclusion series shown and described in Figure 2, originally appearing in the first of the earlier works.
While I still feel this approach is relevant to advancing the cause of an "updated" Spinozian interpretation, it leads to no immediate progress on how a three-dimensional "physical space" milieu might be produced, or how to test any such notion (and, as I stated in the last paper, I now believe it pertains mainly to the attribute "thought"). I have therefore more recently been following another track which seems more productive in this regard. To appreciate this approach we need first study a manner of complementarity of the two fundamental attributes that I feel is consistent with the double "complete representation" restriction of Spinoza's model.
SPACE AS LOGICAL REPRESENTATION
The hierarchical inclusion series sketched above rests on the assumption that each mode within it be logically equivalent. "Logically," because we are not demanding that each system's mode be structurally identical (as might, for example, the several primary atoms of a carbon ring structure), only that it of necessity carry the same "weight" in actualizing the function of the overall system--for example, the human nervous system is entirely distinct from our digestive system, but both are equally necessary to our overall organization. Such logic has, of course, no built-in spatial connotation. Importantly, however, it is entirely possible to impose additional conditions that make possible its re-setting into spatial terms, and to this matter we now turn. The fastest way to examine this question is to quickly explore a real world situation.
Human population within the typical Western regional area distributes itself hierarchically, according to socioeconomic forces governing the population size of the constituent towns and cities; the sustaining inverse function relates size class of center to number of centers present in each such class. Consider the contrived regional setting diagrammed in Figure 3. This consists, as represented, of one large "central" city, five smaller cities, ten large towns, and twenty small towns, coded as such in Figure 3.A. Such classifications are often based on socio-economic function within the overall system, a function that is usually closely related to population size of center.
Figures 3.A, 3.B & 3.C:
Fig. 3.A.
Fig. 3.B.
Fig. 3.C.
Figure 3.B shows how the same basic classification can be arrived at by looking at interaction data. Here, we might be dealing with, for example, commuting data (where dotted lines between centers represent thresholds of fifty trips, dashed lines five hundred, and solid lines five thousand). In this instance, the total number of commutes emanating from the center would identify it with one of the four size levels. In Figure 3.C, however, the same trips data are used to specify a subregional classification, since, independent of size considerations, certain towns and suburbs fall within one or another of the several general "commutersheds" in the region. In this instance, absolute size of center is not such a relevant consideration as compared to nearness--to subregional evolution. The classification shown in Figure 3.C is of a historical type, whereas that shown in 3.A describes organization of an "ecological" type.
Either form of classification of centers into groups can be followed by the calculation of group (class)-level averages. The latter values may then be arranged in matrix form. In the case of the subregional delineation, an idea of the subregional interaction structure is obtained by looking at totals of trips/calls between and within regions. This form of representation (Figure 3.C) can produce an additive inclusion series of (subregional) relations interpretable in hierarchical terms of the type discussed in the last paper (if one wishes to split the regions into finer units, or keep lumping them together into broader ones). Economic function according to size/rank, however, is best examined in relational terms by linking the spatial pattern of centers to principles of shopping behavior and other market-related variables, and to how this arrangement functionally maintains the overall urban hierarchy (as studied, for example, through Central Place Theory). If we make the assumption that population size accurately reflects function in this regard (and on the whole it does), we can generate a classification of size groups a priori, and then examine the way the relative location of all members of any one class to all members of any other class--taken for all combinations of groupings--defines a population clustering pattern supporting the socio-economic superstructure of the overall system.
This ecological classification form has its analogs in various other kinds of systems, whether we measure the internal associations supporting them on the basis of gravitational relationships (solar/planetary systems, topography in drainage basins, etc.), economic functions in social/political systems, or rates of chemical, biochemical, or organismal interaction in physical and biological systems. Indeed, I propose that all structurally integral systems might possibly be organized in such fashion, and that our failure to fully exploit this notion comes in part from the lesser and greater degrees of overt (measurable) differentiation involved from system to system, and in part from our lack of a model accurately reflecting the generalized basis for such organization. Here I should like to sketch out the fundamentals of such a model. Most basically, it poses that the flows of information between/among the basic elements of a functioning system organize themselves de facto into group-level interaction structures--subsystems--which are maintained in the form of a solvable equation whose "solution" corresponds to a three-dimensional spatial projection. All of the remaining discussion here will be devoted to exploring this notion.
Note that Spinozian thinking will cause us to focus on the relations among the subsystems of a given subsystemization, as opposed to any kinds of relation between or among different subsystemizations, or between whole systems (as is often or usually the case with investigations falling within the general Empiricist tradition, which attaches a priority to observable--especially testable--cause and effect over logic of internal structure per se), or whole systems and their more elemental parts (a body and its constituent cells, for example). Recall here the "all of nature in a rose" concept; I suggest that one can approach this wisdom by looking to structural commonalities (i.e., parallels) rather than causal relations between systems.
Structural relations between particular subsystem pairs in a given subsystemization can be expressed in terms of "partial identities" (the varying degrees of similarity or dissimilarities between particular subsystem pairs), or perhaps most ideally as actual net flows of materials or services (as in the earlier commuter trips example)--or information--between/among them. The summary representation of flows or similarities is easily rendered in matrix form; the result is a depiction of subsystem structure that reflects its natural differentiation in terms of such actual or implied flows of information.
But again, such initial depictions do not provide an entropy-maximized view of structure, which dwells on the logical/functional equivalence of the subunits in contributing information essential to persistence of the whole. My idea here is that we may have natural systems--in Spinoza's terminology "modifications"--exhibiting an infinite number of disequilibrial or dynamic equilibrium forms that yet observe a single principle of entropy maximization: organization as a three-dimensional extended space. I suggest that all systems maximize their internal entropy in this common fashion such that the three-dimensional structural framework--but ultimately not their individual selves--is permanently maintained.
Although the preceding concepts are admittedly not (yet) organized about a rigid mathematical or logical framework, they are reasonably tidy conceptually and have the advantage of readily lending themselves to simulation. Simply, one can investigate beforehand what range of measurable (magnitudes of) relations must obtain among the interacting elements within any imaginable system to sustain three-dimensionality, and use this basis as the standard against which studies of real world systems can proceed.
The easiest way to introduce the rationale for the simulations I have performed is to compare them to the general manner of use of the well-known multivariate statistical operation multidimensional scaling (MDS). This starting point helps us in our efforts to "work backwards" from the fact of three-dimensionality to a consideration of the kinds of constraints under which this form of structural expression might be operating. The purpose of MDS is to translate the rated intersimilarities of a set of objects into a corresponding set of coordinate scores distributed within an n-dimensional space--that is, to create a group "spatial projection" of those ratings en masse. MDS algorithms are thus attuned to solving the problem of best-fitting an x by x similarities or dissimilarities matrix to a corresponding Euclidean spatial representation. (Consider this trivial but instructive example: The set of airline distances among 25 American cities, used as input data for an MDS operation, would yield a projection of 25 points whose relative locations in a Euclidean three-dimensional output configuration would correspond exactly to the relative locations of the cities in the real world, including their overall lie along the gently curving surface of the earth.)
Let us now imagine that we have performed an analysis of the spatial pattern affinities among the classes of towns/cities as represented in Figure 3.A, concentrating on the rural-urban hierarchy (i.e., not the subregional organization patterns). If we wish to determine how each size-class of places is the more or the less closely spatially affined with each other size-class, we might apply some measure of spatial autocorrelation to the group patterns involved, eventually arriving at a matrix of values summarizing the varying nature of group-level proximities. At this point arrives the question crucial to present concerns: Will this summary matrix, when projected though an MDS operation, produce a three-dimensional representation of relationships which absorbs all the variance of the initial matrix of values? In other words, can the net sum of relationships among the class structures project directly as a "non-fuzzy" three-dimensional space?
It will, I submit, if three general conditions are met. First, and most fundamentally, if the fact of system subdifferentiation is related to spatial extension in the sense I am suggesting. Second, if we have adequately isolated the extent of the system as it exists and chosen a "complete and unbiassed" means of representing it through appropriate surrogates. Third, if our technical means of measuring the system is itself adequate and our secondary calculations (involving, for example, pattern measures) are reasonably unbiassed.
To summarize: I suggest that "natural" subsystemization within any physically-extended system might correspond to--and actually produce--its projection as a three-dimensional entity. The fundamental limitation on system organization is therefore that the numerical representation of its subdifferentiation of elements must be such as to translate, in sum, into a dimensional representation with specific properties. This, as it turns out, is a fairly severe constraint, since the vast majority of what can be stated in relational, matrix terms will not meet it.
For the present, I must skip over a number of very interesting related and extenuating subjects (e.g., how the "elemental bits" of the sum relations might be organized, why we should expect reality to be expressed as a three-dimensional Euclidean space rather than through some other dimensionality, the representation of different system equilibrium states, etc.) and proceed immediately onward to the aspect of the model focussed on here: its inherent testability.
TESTING THE MODEL: PRELIMINARIES
I believe that the model presented here can be tested through the combination of simulation and natural experiment. A properly conceived set of simulations should identify the range of all possible conditions of system subdifferentiation corresponding to numerical matrix representations that meet the relevant constraint (i.e., producing an unambiguous dimensional outcome). It was hoped initially that many of these matrix representations will not produce projections that meet all conditions set out by the model; in contrast, one would expect actual systems to always produce representations that do (again, it is such projection that I am postulating is extended space). If, of course, it should turn out that all simulated projections observe the conditions, we will be forced to give up the model, or perhaps at most to accept that it has a trivial bearing.
I shall describe the exact simulations I have conducted in the next several write-ups; a few conceptual matters that look ahead to these and empirical applications must be dealt with first.
Consider the following 4 by 4 similarities matrix:
5.000 4.000 2.938 3.775
4.000 5.000 2.062 3.775
2.938 2.062 5.000 3.197
3.775 3.775 3.197 5.000
This matrix of values can be mapped directly through MDS into a three-dimensional output configuration, with no "fuzziness" of representation (i.e., no "stress," or lack of correlation between the original data and the representation) resulting. Although the set of coordinates produced is unambiguously set within a three-dimensional Euclidean space, however, this does not guarantee that it meets the requirements here of creating a "logic-based" space. The MDS coordinate system is a prior reality in which each axis is equally weighted, with any given input matrix then being fit to this independently established system. Thus, we are "forcing" the data to conform to a prior three-dimensional orthogonality. Our intent here, on the other hand, is to let the dimensional representation establish itself through the data, a different problem.
The relational data in the input matrix are usually indicative of measurements of interaction characteristics between classes of things. Just because there may be a greater than average magnitude of "overt" interaction between a given class and all the others doesn't necessarily mean, however, that the class involved is "more important" to defining the system: there may simply be a larger built-in element of redundancy in its information processing function. Transforming the matrix into an entropy-maximized version of itself in which all row and column vectors are standardized assures representation of the classes as logically equivalent entities with respect to the integrity of the sum system (a procedure routinely applied in many fields, e.g. econometric analyses of intra-regional commodity flows or trips data to and from vastly differing-sized places). The entropy maximization procedure I have been using is double-standardization, in which all rows, and then all columns, of an x by x matrix are alternately standardized to z scores as many times as it takes to force the matrix elements to converge to stable values (see Smith [1983a, 1983b] and Slater [1976] for examples of use; many others also exist). Any double-standardized 4 by 4 matrix consisting of symmetric z scores (i.e., where all ij values are the same as their corresponding ji values, and all i=j values are the same) can specify a set of unambiguously-placed three-dimensional coordinates. Such coordinates will either project a (two-dimensional) rectangle centered at 0,0,0, or two pairs of equally spaced and opposed points centered three-dimensionally at 0,0,0, in either case describing an underlying space of the type appropriate to present considerations, as such configurations are three dimensionally symmetric (i.e., their four coordinate points are geometrically indistinguishable from one another once one removes axial affinities).
The similarities matrix displayed above, when double-standardized, converges to the following symmetric set of z scores, which do in fact meet all the criteria just stated:
1.67743 -0.21333 -0.54641 -0.91769
-0.21333 1.67743 -0.91769 -0.54641
-0.54641 -0.91769 1.67743 -0.21333
-0.91768 -0.54641 -0.21333 1.67743
So far I have been speaking as though subsystems were no more than abstractions akin to MDS configurations--points "in space" located at simple linear distances from one another. In the real world, however, the elements of the subsystems (for example, the differing-sized towns in the example given earlier, or the varying elevations that may be areally sampled from within a stream basin) will be distributed in some non-singular fashion. To generate a matrix of relations in such instances that reflects conditions of relative location, it will be necessary to equitably sample, and then apply some measure of average (group level) spatial autocorrelation (or, alternately, use some measure of actual energy flow from location to location). Thus, once the sampled elements are classed into groups on the basis of some independently measurable property (such as population size or elevation), the resulting groups' degrees of spatial autocorrelation with one another can be calculated, and the matricized spatial autocorrelation scores double-standardized. Under the present model, if the resulting z scores are symmetric (all ij = ji, and all i=j scores identical, and highest), the results conform to what is necessary to define a three-dimensionally extended "natural system."
Clearly-defined surrogates that mirror internal system differentiation properties are not that easy to come by. I have found, for example, that population of centers per se provides a reasonably unbiassed measure of internal regional differentiation (i.e., into its classes of town size and function) only until about 1950, at which point progressively vaguer results are obtained. The reason for this, ostensibly, is that in the post-1950 period people have increasingly tended to live in one place and work at some considerable distance away; i.e., they "actually" live "in two places," and residence per se no longer defines a concept appropriate to measuring the present kind of group-level interaction. In this instance, then, the functional significance of the surrogate as measured has changed over time. In another kind of example, in this case related to spatial heterogeneity, the use of elevation above sea level as a surrogate for measuring potential energy conditions within stream basins is confounded by the fact that some parts, at least, of any given basin represent depositional environments despite the fact that, fundamentally, the overall regime constitutes an erosion-mediated observance of the Second Law. Elevation per se is therefore a complex measure of system entropy conditions, and the bias should tend to increase the more the basin contains non-strictly equilibrial environments. (However, and as we shall see later, knowing this actually leaves us with additional opportunities for empiricism-based tests of the overall concept.)
In sum, empirical analyses bearing on the validity of the present model will only be possible if certain precautions are taken. To proceed at all we should begin with a system with recognizable boundaries; we must then have some characteristic of internal differentiation of the system that can be measured (or at the least, logically distinguished) such that a sampling over the areal extent of the system will lead to a classification into subsystem units. If the empirical focus is on spatial patterns (as opposed to straightforward flows data), the spatial autocorrelation properties of the subsystems can then be measured, matricized, double-standardized, and the results examined for conformance to the criteria mentioned.
SIMULATIONS OF THREE-DIMENSIONAL SYSTEM STRUCTURES
One should remember that the "historical" (subregional) and "ecological" (urban hierarchy) conceptualizations of the regional population system sketched in Figure 3 can be based on exactly the same data. The ecological structure in particular is derived from a global hierarchical arrangement; usually, and in the example, socioeconomic function. Let us now ask the question of whether the overt pattern of population distribution associated with such a function--or any analogous one--may not only be "set" in two/three dimensional space, but actually define (be projectable as) that space.
Let us suppose for the moment that we have a perfectly symmetric pyramidal figure consisting of four apexes and four faces. Once we have set such a figure geometrically within a three dimensional coordinate system and retrieved all the distances among point pairings in the projection, we can represent this system of distances as a symmetric matrix whose primary diagonal consists of zeros, with all other elements being some other single value. Now imagine that we are instead given only the matrix of distances, and from it asked to construct the figure. One way of doing this, as alluded to earlier, is to input the matrix elements into a metric multidimensional scaling program and specify a three-dimensional solution. The resulting projection of the distances will yield an unambiguously defined set of coordinate locations identifying the relative positions, in geometric space, of the apexes.
Now imagine any other set of numbers arranged as a symmetric i=4, j=4 matrix, and consider the question: How many such sets will inequivocably project a three-dimensional space, as in the pyramid example above?
To examine this matter, crucial to present considerations, I devised a series of simulations. These are described in the next several write-ups.
REFERENCES
Barrow, John D. and Frank J. Tipler [1986], The Anthropic Cosmological Principle. Clarendon Press, Oxford.
Ehrenfest, Paul [1917], "In what way does it become manifest in the fundamental laws of physics that space has three dimensions?" Proceedings of the Royal Academy, Amsterdam, 20, pp. 200-209.
Gurevich, L. and V. Mostepanenko [1971], "On the existence of atoms in n-dimensional space." Physics Letters, 35A(3), pp. 201-202.
Slater, P. B. [1976], "Hierarchical internal migration regions of France." IEEE Transactions on Systems, Man and Cybernetics, April, pp. 321-324.
Smith, Charles H. [1983a], "A system of world mammal faunal regions I. Logical and statistical derivation of the regions." Journal of Biogeography, 10(5), pp. 455-466.
Smith, Charles H. [1983b], "A system of world mammal faunal regions II. The distance decay effect upon inter-regional affinities." Journal of Biogeography, 10(6), pp. 467-482.
Smith, Charles H. [1986a], "A general approach to the study of spatial systems I. The relational representation of measurable attributes." International Journal of General Systems, 12(4), pp. 359-384.
Smith, Charles H. [1986b], "A general approach to the study of spatial systems II. Two examples of application." International Journal of General Systems, 12(4), pp. 385-400.
Smith, Charles H. [1987], "Note on 'A general approach to the study of spatial systems'." International Journal of General Systems, 13(3), pp. 285-287.
Tangherlini, F. R. [1963], "Schwartzschild Field in n dimensions and the dimensionality of space problem." Nuovo Cimento, 27(3), pp. 636-651.
Whitrow, G. J. [1955], "Why physical space has three dimensions." British Journal for the Philosophy of Science, 6(1), pp. 13-31.
_________________________
Continue to Next Essay
Return
to Writings Menu
Return
to Home
Copyright 2006-2014 by Charles H. Smith.
All rights reserved.
Materials from this site, whole or in part, may not be reposted or otherwise
reproduced for publication without the written consent of Charles H. Smith.
Feedback: charles.smith@wku.edu
http://people.wku.edu/charles.smith/once/syst2.htm