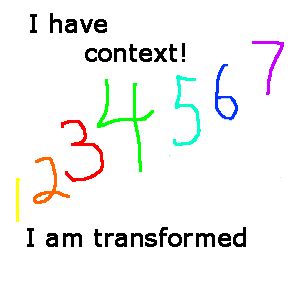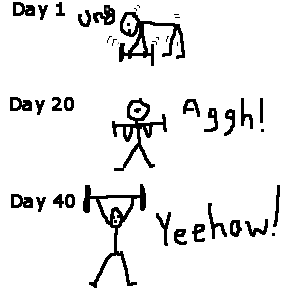Understanding Scores

Overview

• Review types of scores
• Consider standards for comparison

What types of scores are there?

1. Raw Scores
2. Linear Transformed Scores
3. Area Transformed Scores
4. Stanines

What good are they?

The Raw Score

The Raw Score is a simple count of the test behavior, (e.g., # of free throws). It isn't usually meaningful for psychological measures. If I say you have a score of '4,' is that good? Bad? Indifferent? You can't know anything from a simple total. It may sound like a lot or a little, but without knowing how it relates to other information, it is useless.
So we transform it.

Transformation

1. Doesn't change the score, it just uses different units. (Sounds contradictory? wait and see how it works).
2. Transformation includes or takes into account information not in the raw score (such as the # of items on the test).
3. More informative/interpretable than a raw score.

Linear Transformation

Uses the linear equation for the transformation.

Examples:

• z score, mean = 0, sd = 1
• Useful to psychometricians but not for interpretation to lay public because half the scores are negative and often fractional. The public thinks a -.01 is an awful score when really it is average.
• so transform the z scores again to...
  • T scores, mean = 50, sd = 10
  • IQ scores, mean = 100, sd = 15
  • You can pick the mean and sd you like and convert the z to whatever scale you want. But the T and the IQ score are the most common.

So how are these used?

Well, if you know an IQ is 100, you know that person earned a score at the mean of everyone who takes the test.

If the IQ score is 115, you know the person is noticeably above the mean (1 standard deviation= 15. see above).

If 130, much more noticeably above the mean--definitely an unusual score because it is 2 standard deviations from the mean.

How unusual a score is 70? 70 is as unusual as which, 115 or 130?

130-- they're both 2 standard deviations from the mean. Suddenly, by using a linear transformation, the number now has meaning! It tells the unusualness/commoness of a score just by knowing the chosen mean/sd and the score.

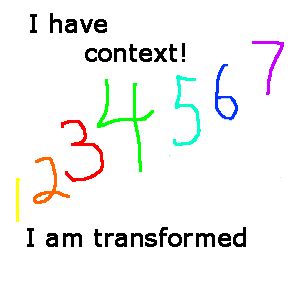Area Transformation

Uses the normal curve to create transformations. An area transformation is where on the curve the score falls, e.g., percentiles (NOT equivalent to percent or percentage).

55^th percentile: earned score equal to or greater than 55 percent of the people who took the test. Notice that phrase 'equal to or greater than.' It has to be exactly that phrase to be accurate.

Percentiles have uneven intervals–Greatly compressed in the middle…stretched at the limits. The difference between 50 and 55 percentile is tiny, but the difference between a 90 and a 95 percentile is huge. Notice that you have to understand the normal distribution to correctly interpret percentile scores.

Standard Nine aka Stanine

• Popular in education.
• The stanine divides the normal curve into 9 segments (Middle 20% scorers = 5; next 17% = 4 or 6; next 12% = 3 and 7; next 7% = 2 and 8; extreme 4% = 1 and 9) [Don't try to memorize that.]
• Not all that useful other than it reduces overinterpretation of scores. In other words, if you tell someone their child had a 72%ile they want to know why they didn't have a 76%ile or want to claim their Johnny is much smarter than Billy who got a 69%ile-- the test probably does not support that fine a distinction. Tell them they had an 8 stanine and that seems to satisfy them.

But what does the number mean in real life?

Depends on what you are using for the standard or comparison. That is, a score is meaningful relative to the comparison on which it is based.

Options for Standards

Personal performance - improvement compared to self over time. You may say "I lift more weight now than I used to." Useful in clinical and some educational work. People like this standard when they are learning--it emphasizes progress made away from the starting point.
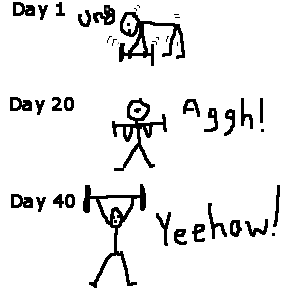External or criterion-referenced. An absolute level of performance must be met to be successful. External agencies often set criterion-referenced standards. This one can seem hard from a learner's point of view. It doesn't matter how hard you tried, how nice you are, or how much you studied. All that matters is whether you can remove an appendix without killing the patient or can land a plane without crashing.
Norm groups- Find out how a group of people do on the test and compare all scores to their performance. This one is used a lot for psychological measures because there often is no external criterion. How much is enough learning? The norm group answer is "As much as everyone else is doing." Learners often like this one because it gives them the security of fitting in. However, they may also rebel at being compared to everyone else.

Since norm groups are so common in psychology, let's explore them a bit further.

Notice that norm groups are also called "standardization samples". Do you see where the concept of standard comes into play?

What group should be used for the norm comparison?

–Depends on what you want to know. Do you want to know how the person is doing compared to a sample of peers, e.g., from the same school? or compared to the US population, e.g., a national group? Do you want to know how they do relative to others their age? or how they'd fit into an older group?

–The sample typically is representative

• of the US population
• of a particular age
• of a particular grade or
• Gender, etc.

But it doesn't have to fit one of the above categories if you have a specific research or clinical question, you need a norm group that reflects your question. My mother had a right hemisphere stroke and I want to know how she is doing. I may want to know relative to other persons with right hemisphere strokes so we can estimate if her pace of improvement is "normal", "slower", or "faster" so we can predict rehabilitation and financial needs.

[Note in this case that there is also an external comparison to be made and considered-- she can either feed herself or not, toilet herself or not. Meeting those standards is necessary for independent functioning. It doesn't matter if she is doing better than the average right hemisphere patient. And relative to herself she has made tremendous improvement, from being confined to bed to being able to walk 100 feet with help. This is great, but it may not be enough for that hard external standard.]

Let's examine the most popular norms.

Age norms

Many psychological traits of interest (e.g., intelligence) change with age so you need a comparison group of the same age.

Crude example: let's say that 5 year olds can define "apple" but 4 year olds can't.

If the subject defines "apple" then she is performing at a "5 year old level"

Grade Norms

Done similarily only with grades. They may say a child is performing similar to the beginning of 3rd grade or similar to the end of 3rd grade.

Typically they just get a beginning and end of year sample, unless it is first or 2nd grade, then they may have a middle. (They limit their samples because they'd have to have a full sample of children for each segment -- it gets costly.)

Big problems with grade norms though

1. "Typical grade tasks" vary considerably w/schools-- so what does "grade" mean anyway? What does it mean to be at the beginning of 3rd grade?
   
2. You absolutely may NOT interpolate (guess at scores between beginning and end of year calculated ones). Why? Because development is not even or regular over the course of the school year. So you can't say child is performing similar to the middle of the year, unless you took a comparison sample from the middle of the year.
   
3. Finally, there's a big problem with "of out of age performance" interpretation…

   Example: a first grader passes "3^rd grade" items.

• This "score" does NOT mean the child is doing 3^rd grade work- means the child is at about 2 or 3 sds for first graders.
  
• Tendency to overgeneralize to other abilities than the tested abilities. ("Janey is outstanding in Math, therefore we don't have to think about her English"-- wrong!)
  
• Generally, avoid using grade norms. Yuck phooey bad norms!

Other considerations

Remember! The particular question you are trying to answer (decision you are trying to make) determines what is the appropriate comparison group. If you are deciding who to take into the US Army, then the potential pool is everyone in the USA. So any selection test standardization sample needs to reflect that. If you are deciding whom to hire in your Bowling Green bakery, you'll be choosing from amongst local Kentuckians and your selection process norm group should reflect that.

Culture Issues

Case ex: I was asked to evaluate for purposes of educational placement an immigrant child who was not doing well in a school in the USA. She didn't speak English. The families intention was to stay in the USA. What norms should be used to evaluate ability? What questions might you need to consider?

What if we changed the situation so that she was returning to her home country in a month for the rest of her life and would need to know where to be placed when she returned home?

To summarize

• Percentiles are commonly used for interpretation to lay population
• Standard scores (z, T, IQ) are favored by professionals because they are less likely to be misinterpreted.
• Occasionally use age norms
• Avoid Grade norms!

Created January 30, 2000: Last Modified: January 30, 2005. All contents© Sally Kuhlenschmidt.