The Once and Future Wallace

Ph.D. Dissertation Postscript

     About twenty-five years have passed since I began work on the preceding Dissertation. Were I to attempt to execute the project today, I would do a lot of things differently, especially as regards data sources and statistical methodologies. The conceptual model, too, might be re-phrased in a number of ways, but on the whole I can't see that its basic logic has in any way been overridden by the events of these last twenty-five years. Indeed, I might argue that many of the ideas that have been introduced since then that bear on related attempts to view evolutionary causalities in terms of environmental forces--for example, the various efforts to relate energy/insolation to productivity and biodiversity--represent oversimplifications, and an actual step backwards to a form of neo-environmental determinism.

     The thing that distinguishes this 1984 effort from all that has followed it is that, whatever its relative primitiveness in many respects, it represents a model of biological change that is directly relatable to state-space conditions. By imagining the process of biological evolution as a kind of information diffusion process spreading at various rates across a metric space, one can deduce various relationships between the two that should admit of test. In my actual Dissertation, I approached this by trying to show, among other things, that on the whole, range boundaries of the species, genera, and families of vertebrates under study should statistically tend to parallel the trends of the isolines defining the information field constructed. This field, it will be remembered, looked like this for the central part of the United States (number magnitudes are dimensionless):

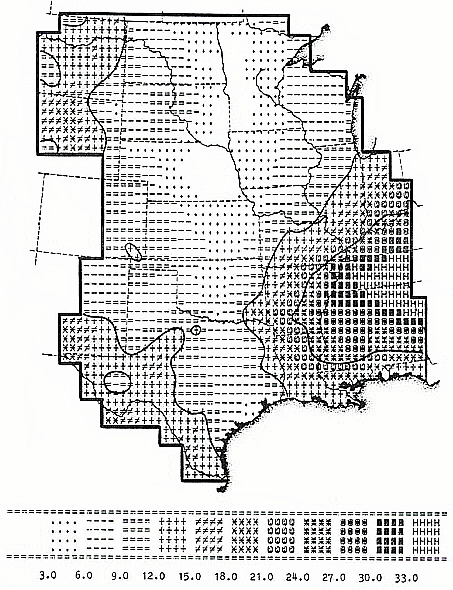
     As it so turned out, the statistical correlations that were predicted were in just about every case produced, though the models in absolute terms were individually weak ones. At the present time much better data are available for distribution patterns, at least, and one might hope for an improvement in model strengths. Beyond this, however, meso-level investigations of gene flow within species populations might be able to expose patterns that could only be anticipated were there in fact clines of information "stress" present--as projected by the model--to produce them.

     I would not be bothering to re-introduce this model if I didn't feel there were some important reasons for thinking about it. One of the most overwhelming influences of the "tree-thinking" of Darwinian approaches to biological evolution is the idea that the products of evolution are, functionally, the sum of species populations that comprise the living world. This idea has carried over, unfortunately, to our treatments of the meaning of biodiversity: practically the first thing that took place after the concept of biodiversity congealed in the late 1980s was a search for, and documentation of, highly biodiverse areas. Naturally, one came to think of such areas as "centers of evolution," and efforts were begun to save these areas from destruction.

     Many things can be said about such "hot spots" of biodiversity that are true enough, including the fact that they contain hordes of unknown or little known species that might actually prove to be of enormous economic value to us, especially insofar as pharmaceutical exploration goes. However, it may be that this emphasis is in part a misplaced one, should it be the case that macroevolution is primarily fired by environmental conditions rather unlike, for example, those sustaining the tropical rainforests. Remember, the essence of the model of evolution described in my Dissertation is one in which the important, macro-level, directions are brought about under conditions of minimal response to "having to be in the right place at the right time" to secure vital resources. In theory, the more such conditions impose on selection, the more the physical or biological environment has brought on a deterministic force of specialization. Otherwise put, it may be the low stress (as I define stress in the Dissertation) areas of the world that are really the "centers of evolution" as a creative force--whatever their actual histories or diversities--whereas in many cases high stress combined with stability only generates repositories of deadend adaptation.

     Now I am supposing that this statement of heresy--that the tropical rainforests, for example, are merely sideshows to the main event of evolution--will elicit titters of laughter from many readers, so I leave you with the results of a new (mid-2006) analysis of my Dissertation data for your consideration. First, note the following map, which shows not only the geographical area I studied in my project, but reproduces the sample grid of some 300+ cells that was used to partition range data into geographical units:

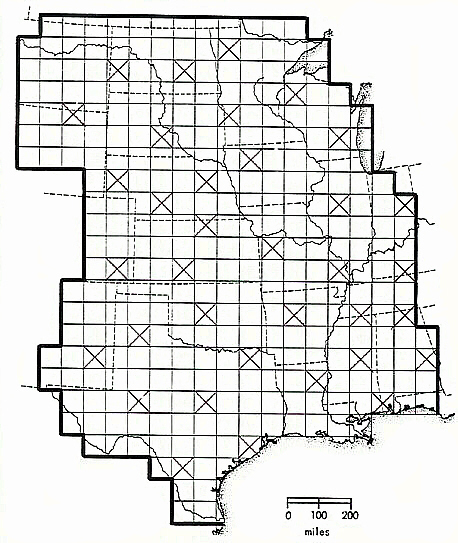
Notice also that thirty-five of the cells have an 'X' struck through them--these are dispersed rather evenly across the whole area (with the exception of the extreme western boundary, which I avoided lest the complication of mountainous areas and their increased diversity due to altitudinal ecological zonation be introduced). For these thirty-five cells I went back and retrieved the mean stress value associated with each, and those species of mammals that could be found in each according to the second edition of Hall's Mammals of North America.

     Generally speaking, I envision a biogeographic evolutionary process in which robustly adapted populations succeed and spread over considerable areas, eventually reaching barriers or physiological limits, and then becoming prone to vicariant events, from which emerge new, derivative, species, usually (and very importantly, only "usually") characterized by greater specialization than the parent population. As one way of looking at this matter, I associated with a "presence" mark in each of the thirty-five cells for a particular species the number of subspecies overall that Hall had identified for that species. A mean score was thus obtained for each cell for the sum of the species in each, by dividing through the total number of subspecies by the diversity of the cell. A linear regression model was then set up in which the mean score was the dependent variable, and the mean stress value for each cell the independent variable.

     Now one should suspect that if there is a strong causal relationship between the environmental conditions at one location and its implications in terms of subspeciation elsewhere (in other words, that that location is inhabited by species that on the whole have sub-diversified to a greater extent) that the regression line here will be negative, and that the associated Pearson correlation coefficient r will be high (and negative). Indeed, both are true for the sample of thirty-five cells taken here, with the r value at -.889. Considering the many possible (and likely) sources of error here, this is a remarkably strong association, even for only thirty-five cases (significant at alpha < .0001). The model is not a perfect one; though the residuals are spread evenly with eighteen negative values and seventeen positives (and the most negative residual is only about 23.5% of the range of the dependent variable, with the most positive residual about 20.5% of the range), there is some correlation between them and the dependent variable, at r = .456. The residuals when mapped show no obvious associations with other factors, however, and this is also a good sign for the basic model.

     I would be interested to hear someone else's explanation as to why this particular measure of environmental stress over an area nearly half the size of the conterminous United States is so good at predicting the degree to which populations (many that extend to beyond that area) subspeciate, if it is not for reasons closely related to those explained in my Dissertation.

     So for the moment I leave the question.

_________________________

Return to Writings Menu
Return to Home

Copyright 2006 by Charles H. Smith. All rights reserved.
Materials from this site, whole or in part, may not be reposted or otherwise reproduced for publication without the written consent of Charles H. Smith.

Feedback: charles.smith@wku.edu
http://people.wku.edu/charles.smith/once/dissadds.htm