The Once and Future Wallace

Simulations: Two-Dimensional Systems.

     In the last writeup a series of simulations was reported in which various groupings of random numbers, collected into n by n matrices, were subjected to the double standardization process I've described. Here, the simulations began with the construction of a series of variously-shaped two-dimensional enclosures, over which a regular triangular-patterned grid was set to establish the locations of a "sample" of points from within the boundaries of the surface. Once the "sample" was collected, the membership of each element at each location was fixed at random by arbitrarily assigning each to one of four classes. It was the spatial autocorrelation properties of the four classes that we were ultimatedly concerned with, and once all class memberships had been established, these data were subjected to the spatial autocorrelation algorithm, summary values produced, and these then double-standardized.

     This basic approach was taken starting with three rather arbitrarily and differently shaped bounded areas, and employing sample sizes of 20, 30, 45, 60, 100, and 405 points. 500 starting configurations were looked at for each of the three 20- and 30-point samplings, and 100 starting configurations were looked at for each of the three 45-, 60-, 100-, and 405 point samplings. The main results may be seen in the following table:

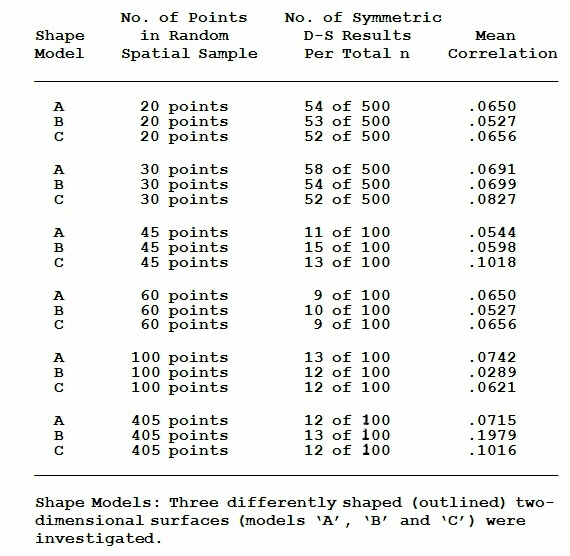
     In this table, "58 of 500" means that 58 of the spatial autocorrelation coefficient matrices out of the 500 tested achieved symmetric results when double-standardized. It should also be noted that these data were compiled many years ago and are afflicted with the same "double-counting" problem I mentioned in the first simulations write-up, on random numbers. So, the actual figures for the rate of passage of the symmetry test are smaller than those given.

     The meaning of these results can be very quickly and easily summarized: regardless of fineness of sample, around the same number of resulting spatial autocorrelation coefficient matrices pass the test; also, it appears that while shape of boundary does not much affect success rate, it does seem to influence the mean correlation of the correlation matrices associated with the s. a. input matrices (as well as several other descriptive statistics, such as number of iterations required to converge). The exact degree to which this is true, and to which this resembles the results for the purely random numbers-based simulations reported in the last write-up, will have to await a re-analysis in which all the categories of outcome are properly separated. Still, it is apparent that these results are, in general, what we would wish to see in "designing" a real-world structural reality: that is, most arbitrary combinations of simulated patterns do not meet the criteria, but a small though nontrivial number do.

_________________________

Continue to Next Essay
Return to Writings Menu
Return to Home

Copyright 2006-2014 by Charles H. Smith. All rights reserved.
Materials from this site, whole or in part, may not be reposted or otherwise reproduced for publication without the written consent of Charles H. Smith.

Feedback: charles.smith@wku.edu
http://people.wku.edu/charles.smith/once/spa3.htm